Tasks
A task unit is a program unit that is obeyed concurrently with the rest of an Ada program. The corresponding activity, a new locus of control, is called a task in Ada terminology, and is similar to a thread, for example in Java Threads. The execution of the main program is also a task, the anonymous environment task. A task unit has both a declaration and a body, which is mandatory. A task body may be compiled separately as a subunit, but a task may not be a library unit, nor may it be generic. Every task depends on a master, which is the immediately surrounding declarative region - a block, a subprogram, another task, or a package. The execution of a master does not complete until all its dependent tasks have terminated. The environment task is the master of all other tasks; it terminates only when all other tasks have terminated.
Task units are similar to packages in that a task declaration defines entities exported from the task, whereas its body contains local declarations and statements of the task.
A single task is declared as follows:
task Single is
declarations of exported identifiers
end Single;
...
task body Single is
local declarations and statements
end Single; A task declaration can be simplified, if nothing is exported, thus:
task No_Exports;
procedure Housekeeping is
task Check_CPU;
task Backup_Disk;
task body Check_CPU is
...
end Check_CPU;
task body Backup_Disk is
...
end Backup_Disk;
-- the two tasks are automatically created and begin execution
begin -- Housekeeping
null;
-- Housekeeping waits here for them to terminate
end Housekeeping;It is possible to declare task types, thus allowing task units to be created dynamically, and incorporated in data structures:
task type T is
...
end T;
...
Task_1, Task_2 : T;
...
task body T is
...
end T;Task types are limited, i.e. they are restricted in the same way as limited private types, so assignment and comparison are not allowed.
Five interlaced pentagons
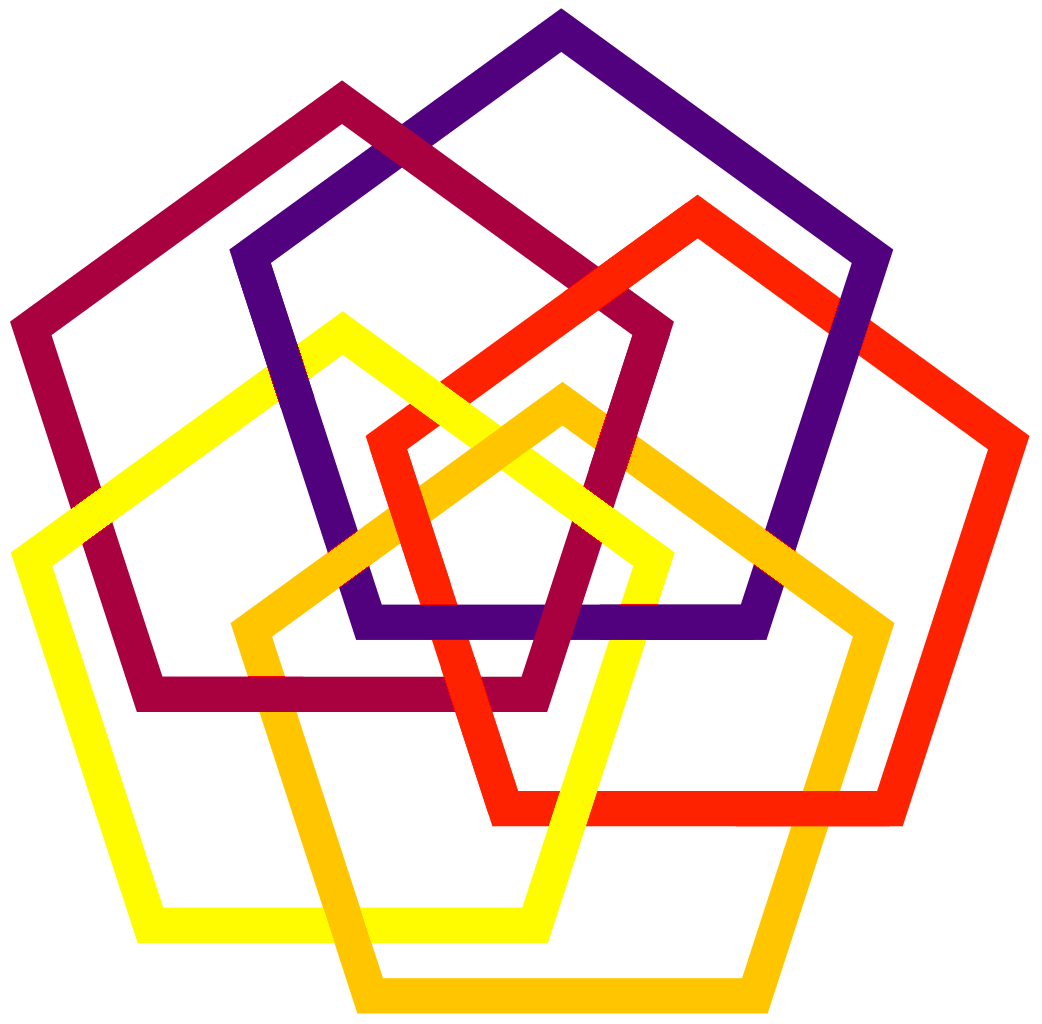
An ornamental design of five alternately interlaced pentagons (a kind of five-fold counterpart to the three-fold Valknut). No two pentagons are directly interlinked, and any three adjacent pentagons (for example, red, blue and turquoise) are in a Borromean rings configuration, which means that two non-adjacent pentagons will have to be removed in order to free the remaining three.
%!
306 396 translate 12.5 setlinewidth/plr{.25 sub 2.47213472 12.5
mul mul dup 3 2 roll 72 mul 90 add dup 3 1 roll cos mul 3 1 roll
sin mul}def/P{4 4 plr 3 4 plr 2 4 plr 1 4 plr 0 4 plr moveto
4{lineto}repeat closepath stroke}def/half{plr currentpoint exch
4 1 roll exch .4 mul exch .6 mul add 3 1 roll .4 mul exch .6 mul
add exch lineto stroke}def
gsave 0 .75 .75 setrgbcolor 3.7526379 2.5 plr translate P grestore
gsave 0 0 1 setrgbcolor 4.7526379 2.5 plr translate P grestore
gsave 1 0 .2 setrgbcolor 0.7526379 2.5 plr translate P grestore
gsave 0 .9 0 setrgbcolor 2.7526379 2.5 plr translate P grestore
gsave 0 .75 .75 setrgbcolor 3.7526379 2.5 plr translate
3 4 plr moveto 2 4 half 2 4 plr moveto 1 4 half
1 4 plr moveto 2 4 half 0 4 plr moveto 1 4 half grestore
gsave 0 0 1 setrgbcolor 4.7526379 2.5 plr translate
3 4 plr moveto 2 4 half 1 4 plr moveto 2 4 half grestore
gsave 1 0 .2 setrgbcolor 0.7526379 2.5 plr translate
4 4 plr moveto 3 4 half 2 4 plr moveto 3 4 half grestore
showpage
%EOFSource: Wikipedia
Plane partition

In mathematics and especially in combinatorics, a plane partition is a two-dimensional array of nonnegative integers $$ n_{i,j}} n_ $$ (with positive integer indices i and j) that is nonincreasing in both indices, that is, that satisfies for all i and j, and for which only finitely many of the ni,j are nonzero. A plane partitions may be represented visually by the placement of a stack of unit cubes above each other giving a three-dimensional solid like the one shown at right.
Source: Wikipedia
Parametric polymorphism
The idea of code reuse arises from the necessity for constructing large software systems combining well-established building blocks. The reusability of code improves the productivity and the quality of software. The generic units are one of the ways in which the Ada language supports this characteristic. A generic unit is a subprogram or package that defines algorithms in terms of types and operations that are not defined until the user instantiates them.
Note to C++ programmers: generic units are similar to C++ templates.
For example, to define a procedure for swapping variables of any (non-limited) type:
generic
type Element_T is private; -- Generic formal type parameter
procedure Swap (X, Y : in out Element_T);procedure Swap (X, Y : in out Element_T) is
Temporary : constant Element_T := X;
begin
X := Y;
Y := Temporary;
end Swap;The Swap subprogram is said to be generic. The subprogram specification is preceded by the generic formal part consisting of the reserved word generic followed by a list of generic formal parameters which may be empty. The entities declared as generic are not directly usable, it is necessary to instantiate them.
To be able to use Swap, it is necessary to create an instance for the wanted type. For example:
procedure Swap_Integers is new Swap (Integer);Now the Swap_Integers procedure can be used for variables of type Integer.
The generic procedure can be instantiated for all the needed types. It can be instantiated with different names or, if the same identifier is used in the instantiation, each declaration overloads the procedure:
procedure Instance_Swap is new Swap (Float);
procedure Instance_Swap is new Swap (Day_T);
procedure Instance_Swap is new Swap (Element_T => Stack_T);Similarly, generic packages can be used, for example, to implement a stack of any kind of elements:
generic
Max: Positive;
type Element_T is private;
package Generic_Stack is
procedure Push (E: Element_T);
function Pop return Element_T;
end Generic_Stack;
package body Generic_Stack is
Stack: array (1 .. Max) of Element_T;
Top : Integer range 0 .. Max := 0; -- initialise to empty
-- ...
end Generic_Stack;A stack of a given size and type could be defined in this way.
Source: Ada Programming
Möbius strip
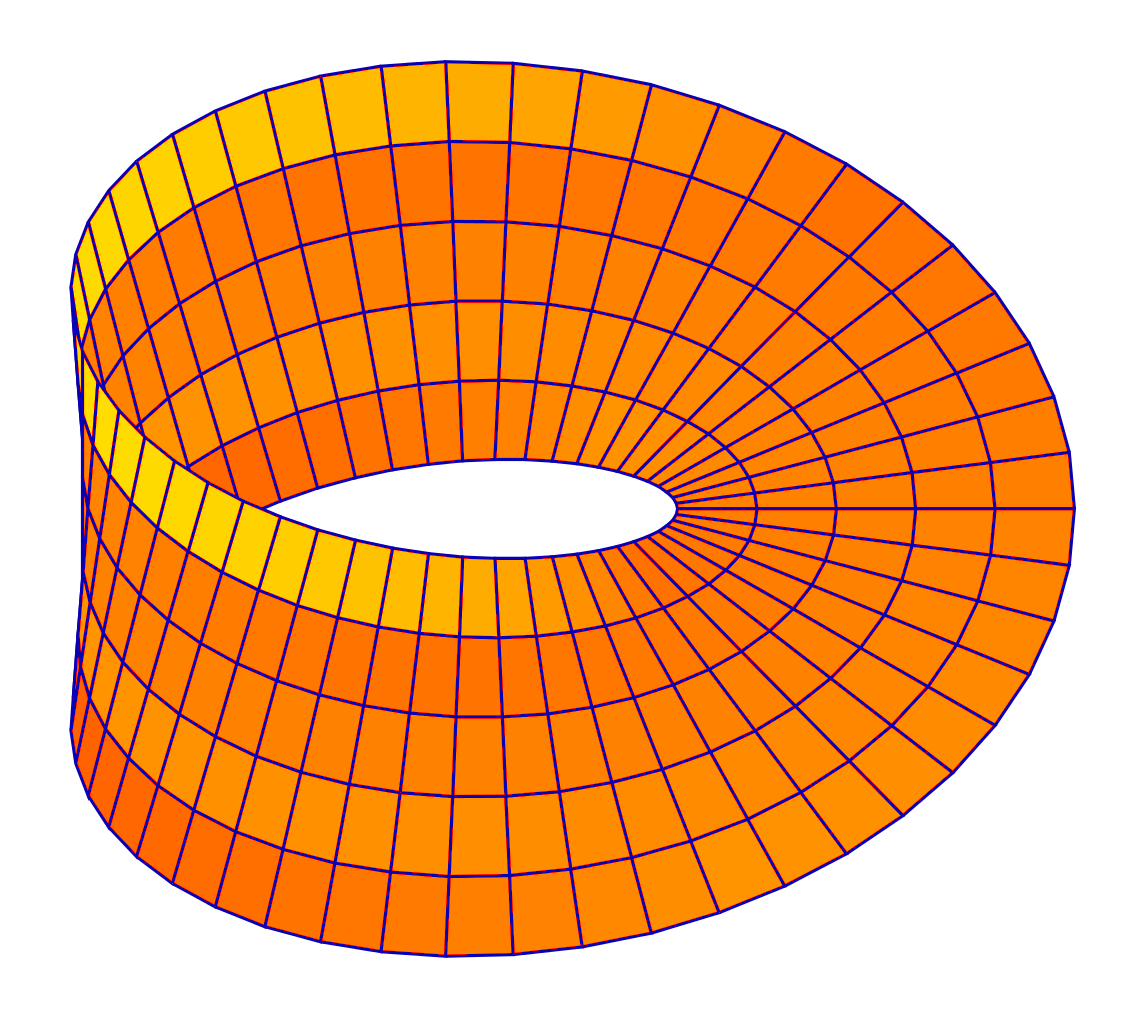 A parametric plot of a Möbius strip
A parametric plot of a Möbius strip
The Möbius strip or Möbius band is a surface with only one side and only one boundary. The Möbius strip has the mathematical property of being non-orientable. It can be realized as a ruled surface. It was discovered independently by the German mathematicians August Ferdinand Möbius and Johann Benedict Listing in 1858.
An example of a Möbius strip can be created by taking a paper strip and giving it a half-twist, and then joining the ends of the strip to form a loop. However, the Möbius strip is not a surface of only one exact size and shape, such as the half-twisted paper strip depicted in the illustration. Rather, mathematicians refer to the closed Möbius band as any surface that is homeomorphic to this strip. Its boundary is a simple closed curve, i.e., homeomorphic to a circle. This allows for a very wide variety of geometric versions of the Möbius band as surfaces each having a definite size and shape. For example, any rectangle can be glued to itself (by identifying one edge with the opposite edge after a reversal of orientation) to make a Möbius band. Some of these can be smoothly modeled in Euclidean space, and others cannot.
A half-twist clockwise gives an embedding of the Möbius strip different from that of a half-twist counterclockwise — that is, as an embedded object in Euclidean space the Möbius strip is a chiral object with right- or left-handedness. However, the underlying topological spaces within the Möbius strip are homeomorphic in each case. There are an infinite number of topologically different embeddings of the same topological space into three-dimensional space, as the Möbius strip can also be formed by twisting the strip an odd number of times greater than one, or by knotting and twisting the strip, before joining its ends. The complete open Möbius band is an example of a topological surface that is closely related to the standard Möbius strip but that is not homeomorphic to it.
It is straightforward to find algebraic equations, the solutions of which have the topology of a Möbius strip, but in general these equations do not describe the same geometric shape that one gets from the twisted paper model described above. In particular, the twisted paper model is a developable surface, having zero Gaussian curvature. A system of differential-algebraic equations that describes models of this type was published in 2007 together with its numerical solution.[4]
Source: Wikipedia
